Multiplication of Egyptian Numbers (Lesson 2)
Unlike the numbers we usually use, it is rather diffcult to do multiplication on Egyptian numerals directly. Therefore, Egyptians found a clever way to get around the diffculty of performing multiplication of two numbers through doubling and addition. Consider the following example:
Example 1.4.
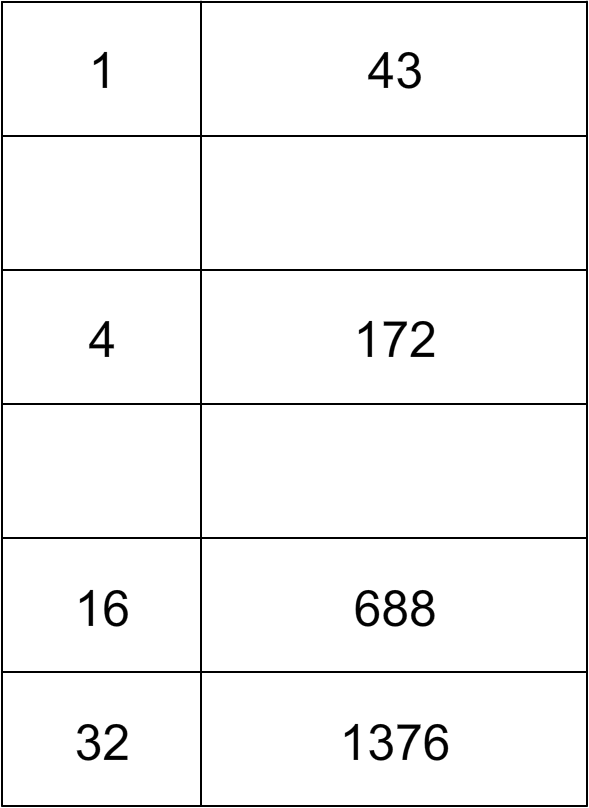
Suppose we want to multiply 53 by 43. First, we double 43 repeatedly (this is quite easily done when using Egyptian numerals). We get the following table

Click to see the Egyptian version
In each row, the number on the left × 43 = the number on the right. We stop the doubling process at "32" because 64 × 43 is already larger than 53 × 43.
Now, starting from 53, subtract it by the largest possible number on the left column i.e., 32, we get 53 - 32 = 21. Then we repeat this process as many times as we can, we get
21 - 16 = 5, 5 - 4 = 1, 1 - 1 = 0
Pick all the rows involved in this process.
Click to see the Egyptian version
We finally add up the numbers on the right in all these rows:
43 + 172 + 688 + 1376 = 2279
and it is your answer! (Do you know why it works? Click the button below for explanation.)
Since by the successive subtractions, we know that 53 = 32 + 16 + 4 + 1 and so
53 × 43 = 32 × 43 + 16 × 43+8 ×43 + 4 × 43 + 1 × 43 = 43 + 172 + 688 + 1376 = 2623
This is also related to the so-called binary number system.